Grover’s Algorithm And Its Variant Algorithm¶
An Introduction to Grover’s Algorithm¶
Grover’s algorithm is a quantum search algorithm for an unstructured database, which was devised by Lov Grover in 1996 (https://arxiv.org/pdf/quant-ph/9605043.pdf). Grover’s algorithm finds the unique input to a black box function that produce a particular output value with high probability, using just \(O(\sqrt{N})\) black boxes. Any classical algorithm cannot solve the search problem in fewer than \(O(N)\) black boxes. In 1997, Bennett, Bernstein, Brassard, and Vazirani proved that any quantum algorithm needs to use black boxes \(\Omega(\sqrt{N})\) times (https://arxiv.org/pdf/quant-ph/9701001.pdf), which means Grover’s algorithm is asymptotically optimal.
Main steps of Grover’s algorithm
Consider an unstructured database with \(N\) entries. There are \(N=2^n\) quantum basis states \(|1\rangle,|2\rangle, \ldots, |N\rangle\), and only the target state \(|\tau\rangle\) is the solution of search problem. Grover’s algorithm consists of following steps:
Initialization. Apply Walsh-Hadamard transformation \(W=H^{\otimes n}\) on the first \(n\) qubits and get the initial state
\[|\psi_0\rangle=W|0\rangle=\sqrt{1/N}\sum_{i=1}^n|i\rangle.\]Perform Grover iteration \(O(\sqrt{N})\) times, measure the first \(n\) qubits and get \(|\tau\rangle\) with high probability. The Grover iteration contains four steps: > Step 1. Flip the phase of target state \(|\tau\rangle\), i.e., apply
\[I_{\tau}=I-2|\tau\rangle\langle \tau |.\]> > Step 2. Apply Walsh-Hadamard transformation \(W=H^{\otimes n}\) on the first \(n\) qubits. > > Step 3. Flip the phase of initial states \(|0\rangle^{\otimes n}\), i.e., apply
\[I_0=2|0\rangle^{\otimes n~n \otimes}\langle 0|-I.\]> > Step 4. Apply Walsh-Hadamard transformation \(W=H^{\otimes n}\) on the first \(n\) qubits.
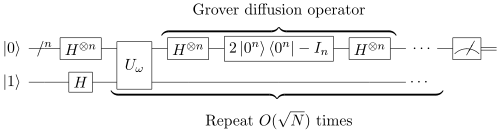
The quantum circuit of Grover’s algorithm is:
Realization of Grover’s Algorithm on HiQ
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 | import math
from projectq.ops import H, Z, X, Measure, All, Ph
from projectq.meta import Loop, Compute, Uncompute, Control
from projectq.cengines import (MainEngine,
AutoReplacer,
LocalOptimizer,
TagRemover,
DecompositionRuleSet)
from hiq.projectq.cengines import GreedyScheduler, HiQMainEngine
from hiq.projectq.backends import SimulatorMPI
import projectq.setups.decompositions
from mpi4py import MPI
"""
To run example use the command line:
$ mpirun -np 4 python ./grover_mpi.py
"""
def run_grover(eng, n, oracle):
"""
Runs Grover's algorithm on n qubit using the provided quantum oracle.
Args:
eng (MainEngine): Main compiler engine to run Grover on.
n (int): Number of bits in the solution.
oracle (function): Function accepting the engine, an n-qubit register,
and an output qubit which is flipped by the oracle for the correct
bit string.
Returns:
solution (list<int>): Solution bit-string.
"""
x = eng.allocate_qureg(n)
# start in uniform superposition
All(H) | x
# number of iterations we have to run:
num_it = int(math.pi / 4. * math.sqrt(1 << n))
print("Number of iterations we have to run: {}".format(num_it))
# prepare the oracle output qubit (the one that is flipped to indicate the
# solution. start in state 1/sqrt(2) * (|0> - |1>) s.t. a bit-flip turns
# into a (-1)-phase.
oracle_out = eng.allocate_qubit()
X | oracle_out
H | oracle_out
# run num_it iterations
with Loop(eng, num_it):
# oracle adds a (-1)-phase to the solution
oracle(eng, x, oracle_out)
# reflection across uniform superposition
with Compute(eng):
All(H) | x
All(X) | x
with Control(eng, x[0:-1]):
Z | x[-1]
Uncompute(eng)
All(Ph(math.pi / n)) | x
All(Measure) | x
Measure | oracle_out
eng.flush()
# return result
return [int(qubit) for qubit in x]
def alternating_bits_oracle(eng, qubits, output):
"""
Marks the solution string 0,1,0,..... by flipping the
qubit,
conditioned on qubits being equal to the alternating bit-string.
Args:
eng (MainEngine): Main compiler engine the algorithm is being run on.
qubits (Qureg): n-qubit quantum register Grover search is run on.
output (Qubit): Output qubit to flip in order to mark the solution.
"""
with Compute(eng):
X | qubits[1]
with Control(eng, qubits):
X | output
Uncompute(eng)
if __name__ == "__main__":
# create a main compiler engine with a simulator backend:
backend = SimulatorMPI(gate_fusion=True,num_local_qubits=20)
cache_depth = 10
rule_set = DecompositionRuleSet(modules=[projectq.setups.decompositions])
engines = [TagRemover()
, LocalOptimizer(cache_depth)
, AutoReplacer(rule_set)
, TagRemover()
, LocalOptimizer(cache_depth)
, GreedyScheduler()
]
eng = HiQMainEngine(backend, engines)
if MPI.COMM_WORLD.Get_rank() == 0:
print("=====================================================================")
print("= This is the Grover algorithm demo")
print("= Change the list to search by modifying alternating_bits_oracle")
print("= The chosen list is: [0, 1, 0, ....]")
print("= The second element is marked")
print("= Calling Grover algorithm to find the marked element now...")
# run Grover search to find a 7-bit solution
N = 7
mark_bits = run_grover(eng, N, alternating_bits_oracle)
if MPI.COMM_WORLD.Get_rank() == 0:
found = False
for i in range(len(mark_bits)):
if mark_bits[i] == 0:
print("= Marked element is found, its index is: {}".format(i))
found = True
if not found:
print("= Cannot find the marked element!")
print("=====================================================================")
|
An Introduction to Exact Grover’s Algorithm¶
Standard Grover’s algorithm can only return the solution of search problem with high probability. In 2001, Lov proposed a modified Grover’s algorithm which can output the solution with probability 1 (https://arxiv.org/pdf/quant-ph/0106071.pdf).
The standard Grover iteration is
\[G=-H^{\otimes n}(I-2|0\rangle\langle 0|)H^{\otimes n}(I-2|\tau\rangle \langle \tau|),\]
where \(\tau\) is the solution of search problem.
The Grover iteration of exact Grover’s algorithm is described as
\[G(\theta, \phi)=-H^{\otimes n}(I+(e^{i\theta}-1)|0\rangle\langle 0|)H^{\otimes n}(I+(e^{i\phi}-1)|\tau\rangle \langle \tau|).\]
Here, \(\theta\) and \(\phi\) satisfy:
\[\cot ((2m+1)\beta)=e^{i\phi}\sin(2\beta)(-\cos(2\beta)+i\cot(\theta/2))^{-1},\]
where \(m=\pi 2^{n-2}\) and \(\sin^2(\beta)=1/2^{n}\).
Realization of Exact Grover’s Algorithm on HiQ
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 | import math
from projectq.ops import H, Z, X, Measure, All, Ph, Rz
from projectq.meta import Loop, Compute, Uncompute, Control
from projectq.backends import CircuitDrawer, CommandPrinter
from projectq.cengines import (MainEngine,
AutoReplacer,
LocalOptimizer,
TagRemover,
DecompositionRuleSet)
import projectq.setups.decompositions
from hiq.projectq.backends import SimulatorMPI
from hiq.projectq.cengines import GreedyScheduler, HiQMainEngine
from mpi4py import MPI
def run_exactgrover(eng, n, oracle, oracle_modified):
"""
Runs exact Grover's algorithm on n qubit using the two kind of provided
quantum oracles (oracle and oracle_modified).
This is an algorithm which can output solution with probability 1.
Args:
eng (MainEngine): Main compiler engine to run Grover on.
n (int): Number of bits in the solution.
oracle (function): Function accepting the engine, an n-qubit register,
and an output qubit which is flipped by the oracle for the correct
bit string.
Returns:
solution (list<int>): Solution bit-string.
"""
x = eng.allocate_qureg(n)
# start in uniform superposition
All(H) | x
# number of iterations we have to run:
num_it = int(math.pi/4.*math.sqrt(1 << n))
#phi is the parameter of modified oracle
#varphi is the parameter of reflection across uniform superposition
theta=math.asin(math.sqrt(1/(1 << n)))
phi=math.acos(-math.cos(2*theta)/(math.sin(2*theta)*math.tan((2*num_it+1)*theta)))
varphi=math.atan(1/(math.sin(2*theta)*math.sin(phi)*math.tan((2*num_it+1)*theta)))*2
# prepare the oracle output qubit (the one that is flipped to indicate the
# solution. start in state 1/sqrt(2) * (|0> - |1>) s.t. a bit-flip turns
# into a (-1)-phase.
oracle_out = eng.allocate_qubit()
X | oracle_out
H | oracle_out
# run num_it iterations
with Loop(eng, num_it):
# oracle adds a (-1)-phase to the solution
oracle(eng, x, oracle_out)
# reflection across uniform superposition
with Compute(eng):
All(H) | x
All(X) | x
with Control(eng, x[0:-1]):
Z | x[-1]
Uncompute(eng)
# prepare the oracle output qubit (the one that is flipped to indicate the
# solution. start in state |1> s.t. a bit-flip turns into a e^(i*phi)-phase.
H | oracle_out
oracle_modified(eng, x, oracle_out, phi)
with Compute(eng):
All(H) | x
All(X) | x
with Control(eng, x[0:-1]):
Rz(varphi) | x[-1]
Ph(varphi/2) | x[-1]
Uncompute(eng)
All(Measure) | x
Measure | oracle_out
eng.flush()
# return result
return [int(qubit) for qubit in x]
def alternating_bits_oracle(eng, qubits, output):
"""
Marks the solution string 0, 1, 0,...,0 by flipping the
qubit,
conditioned on qubits being equal to the alternating bit-string.
Args:
eng (MainEngine): Main compiler engine the algorithm is being run on.
qubits (Qureg): n-qubit quantum register Grover search is run on.
output (Qubit): Output qubit to flip in order to mark the solution.
"""
with Compute(eng):
X | qubits[1]
with Control(eng, qubits):
X | output
Uncompute(eng)
def alternating_bits_oracle_modified(eng, qubits, output, phi):
"""
Marks the solution string 0,1,0,... by applying phase gate to the output bits,
conditioned on qubits being equal to the alternating bit-string.
Args:
eng (MainEngine): Main compiler engine the algorithm is being run on.
qubits (Qureg): n-qubit quantum register Grover search is run on.
output (Qubit): Output qubit to mark the solution by a phase gate with parameter phi.
"""
with Compute(eng):
All(X) | qubits[1::2]
with Control(eng, qubits):
Rz(phi) | output
Ph(phi/2) | output
Uncompute(eng)
if __name__ == "__main__":
# create a main compiler engine with a simulator backend:
backend = SimulatorMPI(gate_fusion=True, num_local_qubits=20)
# backend = CircuitDrawer()
# locations = {}
# for i in range(module.nqubits):
# locations[i] = i
# backend.set_qubit_locations(locations)
cache_depth = 10
rule_set = DecompositionRuleSet(modules=[projectq.setups.decompositions])
engines = [TagRemover(),
LocalOptimizer(cache_depth),
AutoReplacer(rule_set),
TagRemover(),
LocalOptimizer(cache_depth)
#,CommandPrinter()
, GreedyScheduler()
]
eng = HiQMainEngine(backend, engines)
# run Grover search to find a 7-bit solution
print("=====================================================================")
print("= This is the Grover algorithm demo")
print("= Change the list to search by modifying alternating_bits_oracle")
print("= The chosen list is: [0, 1, 0, ....]")
print("= The second element is marked")
print("= Calling ExactGrover algorithm to find the marked element now...")
# run Grover search to find a 7-bit solution
N = 12
mark_bits = run_exactgrover(eng, N, alternating_bits_oracle, alternating_bits_oracle_modified)
found = False
for i in range(len(mark_bits)):
if mark_bits[i] == 0:
print("= Marked element is found, it index is: {}".format(i))
found = True
if not found:
print("= Cannot found the marked element!")
print("=====================================================================")
|
References:
[1] Grover L K. A fast quantum mechanical algorithm for database search[C]//
Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. ACM, 1996: 212-219.
[2] Brassard G, Hoyer P, Mosca M, et al. Quantum amplitude amplification and estimation[J]. Contemporary Mathematics, 2002, 305: 53-74.