Phase Estimation

Introduction

Problem Description

The quantum phase estimation algorithm is a quantum algorithm used to estimate the phase (or eigenvalue) of an eigenvector of a unitary operator. More precisely, given a unitary matrix \(U\) and a quantum state \(\vert\psi\rangle\) such that \(U\vert\psi\rangle=e^{2\pi i\theta}\vert\psi\rangle\) (that is, \(\vert\psi\rangle\) is an eigenstate of \(U\)) and \(\theta\in[0,1)\), the algorithm estimates the value of \(\theta\) with high probability within additive error \(\varepsilon\), using \(O(1/\varepsilon)\) controlled-\(U\) operations.

Note: We can write the eigenvalue of \(U\) in the form \(e^{2\pi i\theta}\) because \(U\) is a unitary operator over a complex vector space, so its eigenvalues must be complex numbers with absolute value \(1\).

Blackbox (aka. Oracles)

To perform the estimation we assume that we have available blackbox capable of preparing the state \(\vert\psi\rangle\) and performing the controlled-\(U^{2^j}\) operation for suitable \(j\in\mathbb{Z}^+\).

Input

The input consists of two quantum registers:

First, the upper \(n\) qubits comprise the first register. This register is used to store the value of \(\left\lfloor 2^n\theta \right\rfloor\). If we express \(\theta\) in the binary form: \(\theta=0. \theta_0\theta_1\cdots\), then \(\left\lfloor 2^n\theta \right\rfloor = \theta_0\theta_1\cdots\theta_{n-1}\). The \(n\) qubits stores the \(n\) binaries \(\theta_i\). The choice of \(n\) depends on two things: the number of digits of accuracy we wish to have for the estimation of \(\theta\), and with what probability we wish the estimation algorithm to be successful. There is a tradeoff between accuracy and probability.

Second, the lower \(m\) qubits are the second register, which stores the input state \(\vert\psi\rangle\). It keeps unchanged throughout the algorithm.

The Circuit

The quantum circuit for phase estimation is shown as follows (excerpted from Wikipedia)

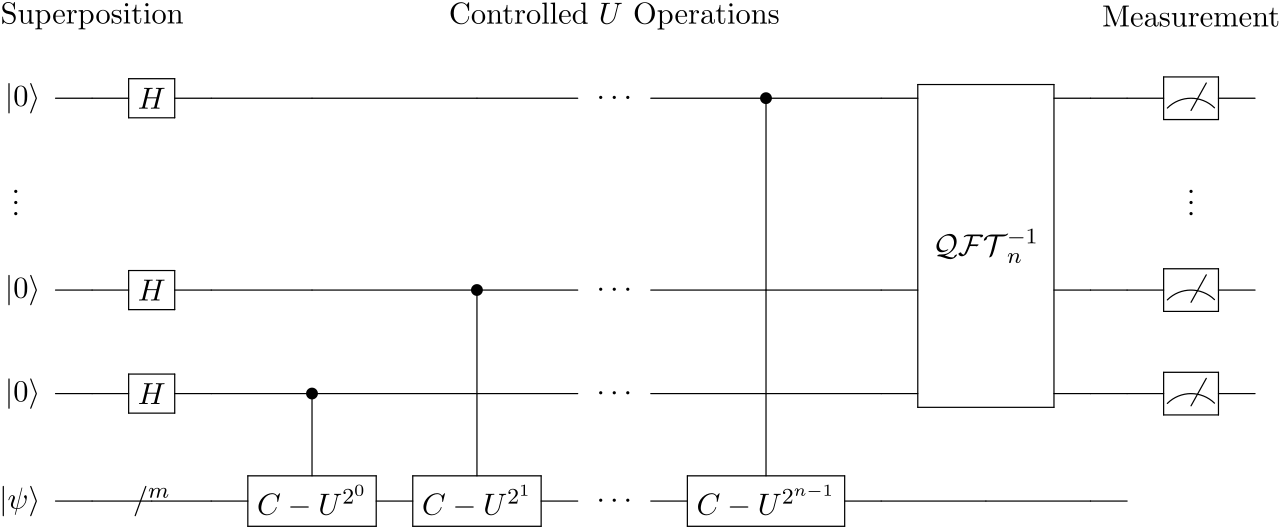
We analyze the circuit step by step. We use \(\vert\Psi_t\rangle\) to represent the state of the system after \(t\) steps. The initial system state is given by

\[\vert\Psi_0\rangle = \vert0\rangle_n\otimes\vert\psi\rangle.\]

Step 1. Create a superposition.

As most quantum algorithms do, we put the initial state of the first register into a superposition. After Step 1, the system state becomes

\[\vert\Psi_1\rangle = \frac{1}{\sqrt{2n}}\sum_{t=0}^{2^n-1}\vert t \rangle \vert \psi \rangle.\]

Here we assume \(t\) is expressed in its binary form.

Step 2. Apply controlled unitary operations.

It is easy to verify that

\[U^{2j}\vert\psi\rangle = U^{2j-1}e^{2\pi i\theta}\vert\psi\rangle = \cdots = e^{2\pi i 2^j\theta}\vert\psi\rangle.\]

Assume the binary expansion of \(t = t_0\cdots t_{n-1}\), each \(t_i\in\{0,1\}\), we have

\[\operatorname{C-U}\left(\vert t \rangle\vert\psi\rangle\right) = \vert t \rangle\left(\prod_{i=0}^{n-1} U^{2^{i}\times t_i}\right)\vert\psi\rangle = \vert t \rangle U^{t}\vert\psi\rangle = e^{2\pi i t\theta}\vert t\rangle\vert\psi\rangle.\]

After Step 2, the system state becomes

\[\vert\Psi_2\rangle = \frac{1}{\sqrt{2^n}}\sum_{t=0}^{2^n-1}e^{2\pi i t\theta}\vert t \rangle\vert \psi\rangle.\]

As we can see, by applying controlled unitaries, we map \(\theta\) to the amplitude of the state.

Step 3. Apply inverse Quantum Fourier transform.

Further analyzing \(\vert\Psi_2\rangle\), we find that it can be obtained from state \(\vert\theta\rangle\vert\psi\rangle\) by performing a quantum Fourier transform on the first quantum register (with some error). Now we perform a inverse quantum Fourier transform on \(\vert\Psi_2\rangle\) (particularly, on state \(\vert t\rangle\)), we obtain

\[\vert\Psi_3\rangle = \frac{1}{\sqrt{2^n}} \sum_{t=0}^{2^n-1} e^{2\pi i t\theta} \left( \frac{1}{\sqrt{2^n}} \sum_{x=0}^{2^n-1} e^{\frac{-2\pi i t x}{2^n}} \vert x\rangle \right) \vert\psi\rangle = \frac{1}{2^n} \sum_{t=0}^{2^n-1}\sum_{x=0}^{2^n-1} e^{-\frac{2\pi it}{2^n}\left(x - 2^n\theta\right)}\vert x\rangle\vert\psi\rangle.\]

Without loss of generality, we can assume \(2^n\theta = a + 2^n\delta\), where \(a\) is the nearest integer to \(2^n\theta\). The difference \(2^n\delta\) satisfies \(0 \leq 2^n\delta \leq 1/2\) (guaranteed by the fact that \(a\) is the nearest integer to \(2^n\theta\)). With this expansion, \(\vert\Psi_3\rangle\) can be rewritten as

\[\vert\Psi_3\rangle = \frac{1}{2^n} \sum_{t=0}^{2^n-1}\sum{x=0}^{2^n-1} e^{-\frac{2\pi it}{2^n}\left(x - a - 2^n\delta\right)}\vert x \rangle\vert\psi\rangle = \frac{1}{2^n} \sum_{t=0}^{2^n-1}\sum_{x=0}^{2^n-1} e^{-\frac{2\pi it}{2^n}\left(x - a\right)}e^{2\pi it \delta} \vert x\rangle\vert\psi\rangle.\]

Step 4. Measurement.

Now we perform a measurement in the standard basis on the first register. We obtain outcome \(\vert a\rangle\) with probability

\[\operatorname{Pr}\left(\vert a \rangle\right) = \left\vert \langle a \vert\Psi_3\rangle \right\vert^2 = \frac{1}{2^{2n}}\left\vert\sum_{t=0}^{2^n-1}e^{2\pi it \delta} \right\vert^2 = \frac{1}{2^{2n}}\left\vert \frac{1- e^{2\pi i 2^n\delta}}{1 - 2^{2\pi i\delta}} \right\vert^2\]

• Case 1. :math:`delta = 0`. In this case, the approximation is precise, we always measure the accurate value of the phase: \(\theta = a/2^n\). The state of the system after the measurement is \(\vert a \rangle\otimes\vert \psi \rangle\).

• Case 2. :math:`delta neq 0`. In this case, we have to lower bound the probability \(\operatorname{Pr}\left(\vert a \rangle\right)\). Since \(2^n\delta\leq 1/2\), the algorithm yields the correct result with probability

  \[\operatorname{Pr}\left(\vert a \rangle\right) \geq \frac{4}{\pi^2} \approx 0.405\]

  This result shows that we can measure the best \(n\)-bit estimate of \(\theta\) with high probability. By increasing the amount of qubits \(n\) by \(O(\log(1/\epsilon))\) and ignoring those last qubits we can increase the probability to \(1-\epsilon\).

HiQ Implementation

Based on the Introduction, we need to be able to implement the following operations:

First, controlled unitary operations. This can be done on the HiQ using the Control meta.

Second, unitary operation raised to some power. This can be done on the HiQ using the Loop meta.

Third, inversed QFT. This can be done on the HiQ by calling get_inverse(QFT), as QFT is already a built-in operation.

We first write a function to calculate the number of bits required to estimate \(\theta\) accurate to n bits with probability of success at least \(1 - \epsilon\). The analytic expression can be found in Nielsen Book, Eq. (5.35):

def _bits_required_to_achieve_accuracy(n, epsilon):
    tmp = math.log2(2 + 1/(2*epsilon))
    tmp = math.ceil(tmp)
    n_updated = int(n + tmp)
    return n_updated

Now we write the main routine used to implement Steps 1-3. We remark that Step 4 is not necessary if we use phase estimation as a subroutine for other algorithms, and this is why we do not count it in the main routine.

def run_phase_estimation(eng, U, state, m, n):
    """
    Phase estimation algorithm on unitary U.
    Args:
        eng (MainEngine): Main compiler engine to run the phase_estimation algorithm
        U (np.matrix): the unitary that is to be estimated
        state (qureg): the input state, which has the form |psi> \otimes |0>.
               Similar to the Introduction, state is composed of two parts:
                 1. The first m qubits are the input state |psi>
                 2. The last n qubits are initialized to |0>, which is used to
                    store the binary digits of the estimated phase
        m (int): number of qubits for input state psi
        n (int): number of qubits used to store the phase to given accuracy
    """
    # The beginning index for the phase qubits will have an offset
    OFFSET = m
    # Step 1 and 2. Create a superposition and perform the controlled U^{2^j} operations
    for k in range(n):
        H | state[OFFSET+k]

        with Control(eng, state[OFFSET+k]):
            # number of loops required to perform the controlled U^{2^j} operation
            num = int(math.pow(2, k))
            with Loop(eng, num):
                U | state[:OFFSET]

    # Step 3. Perform the inverse QFT operation
    # Step 4. Swap the qubits
    for k in range(math.floor(n/2)):
        Swap | (state[OFFSET+k], state[OFFSET+n-k-1])
    # Step 5. Perform the original inverse QFT
    get_inverse(QFT) | state[OFFSET:]

Remark: The default HiQ implementation of QFT ignores the SWAP operations required (see the caption of Figure 5.1 in Nielsen Book). Here we must explicitly call the SWAP operations to swap the qubits and then perform the inversed QFT.

After the run_phase_estimation function, the estimated phase is stored in the last n qubits of the state variable. We can either measure it (This is Step 4 in introduction), or we can use it as the input to other routines.

References:

[1]Wikipedia, Quantum phase estimation algorithm

[2]Nielsen, M., & Chuang, I. (2010). Quantum Computation and Quantum Information: 10th Anniversary Edition.